L1-python/source/Exercice-solution.ipynb

Exercice

import pandas as pd
import numpy as np
from scipy.optimize import curve_fit

Data generation

# constants
g = 10.
V0 = 1.
H = 1.

# Model 
l = V0 * np.sqrt(2.*H/g)

Données

pour file "V1msHvariable.csv"

#
error = 0.01
for h in [0.8, 0.9,1,1.1,1.2]:
    l = V0 * np.sqrt(2.*h/g)
    print('{0:.2f} {1:0.2f} {2:.2f}'.format(l,h,error))

0.40 0.80 0.01
0.42 0.90 0.01
0.45 1.00 0.01
0.47 1.10 0.01
0.49 1.20 0.01

Données

pour file "H1mVvariable.csv"

error = 0.1
for v in [1, 1.2,1.5,2,3]:
    l = v * np.sqrt(2.*H/g)
    print('{0:.2f} {1:0.2f} {2:.2f}'.format(l,v,error))

0.45 1.00 0.10
0.54 1.20 0.10
0.67 1.50 0.10
0.89 2.00 0.10
1.34 3.00 0.10

Solution

# import image module
from IPython.display import Image
  
# get the image
Image(url="experience.png", width=500, height=500)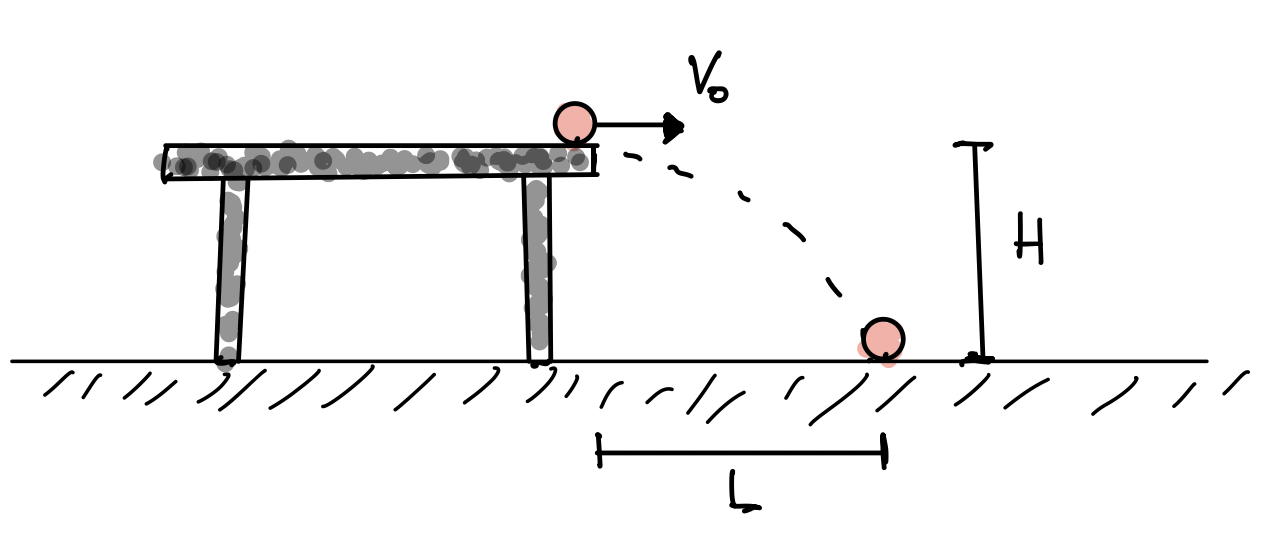

Une bille supposée ponctuelle avec une vitesse horizontale V0V_0 tombe d'une table de hauteur HH et rencontre le sol à une longueur LL.

Nous disposons de deux fichiers de mesures expérimentales (fichiers formatés csv séparés par des ";")

• "V1msHvariable.csv" expérience de mesure de la longueur LL à vitesse V0=1m/sV_0=1 \ m/s constante pour des différentes hauteurs HH avec l'erreur correspondante
• "H1mVvariable.csv" expérience de mesure de la longueur LL à hauteur H=1mH= 1 \ m constante pour des différentes vitesses V0V_0 avec l'erreur correspondante

On propose un modèle pour la longueur LL

L=CV0αHβ L = C V_0^\alpha H^\beta

nous allons évaluer les coefficients α\alpha et β\beta, ainsi que la constante CC.

Point 1.1

En utilisant la bibliothèque Pandas, lisez le fichier "V1msHvariable.csv" et définisez les variables LL, HH, et erreurerreur (de la mesure de hauteur)

d = pd.read_csv("V1msHvariable.csv",delimiter=";")
print(d)

      L    H  error
0  0.40  0.8   0.01
1  0.42  0.9   0.01
2  0.45  1.0   0.01
3  0.47  1.1   0.01
4  0.49  1.2   0.01

d.head()
# taking values from headers
L = d["L"]
H = d["H"]
e =  d["error"]

Point 1.2

Faites une figure de LL vs HH avec barres d'erreur

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(6,6)) # s
ax = plt.subplot() 
ax.errorbar(H,L,e, marker='.', linestyle="none", label="data")
ax.set_title("L vs H")
ax.set_xlabel("H[m]")
ax.set_ylabel("L[m]")
ax.legend()

<matplotlib.legend.Legend at 0x7f84498dfc70>

Point 1.3

Utilisez la fonction "curve_fit" pour faire une regression linéaire des données exprimées en une échelle log-log et trouve la valeur de α\alpha

# fit
def func(x, a, b):
    return a * x + b

from scipy.optimize import curve_fit

popt= curve_fit(func, np.log(H), np.log(L))

popt[0]
a=popt[0][0]
b=popt[0][1]
print("a = %.3f" % a)
print("b= %.3f" % b)

a = 0.512
b= -0.805

Point 1.4

Faites un figure log-log de LL vs HH en ajoutant la regression linéaire trouvée dans le point précédent

fig = plt.figure(figsize=(6,6)) # s
ax = plt.subplot() 
ax.errorbar(H,L,e, marker='.', linestyle="none", label="data")
ax.plot(H,np.exp(b)*H**a,"-",label="model")
ax.set_title("with error bars")
ax.set_title("L vs H")
ax.set_xlabel("H[m]")
ax.set_ylabel("L[m]")
ax.legend()
ax.loglog()

[]

Estimation de la constante CC

C=L/H**0.5
print(C)

0    0.447214
1    0.442719
2    0.450000
3    0.448127
4    0.447307
dtype: float64

Partie 2

Etude de la longueur LL à hauteur H=1mH= 1 \ m constante pour des différentes vitesses V0V_0

Point 2.1

En utilisant la bibliothèque Pandas, lisez le fichier "H1mVvariable.csv" et définisez les variables LL, V0V_0, et erreurerreur (de la mesure de vitesse)

d = pd.read_csv("H1mVvariable.csv",delimiter=";")
print(d)

      L    V  error
0  0.45  1.0    0.1
1  0.54  1.2    0.1
2  0.67  1.5    0.1
3  0.89  2.0    0.1
4  1.34  3.0    0.1

# taking values from headers
L = d["L"]
V = d["V"]
e =  d["error"]

Point 2.2

Faites une figure de LL vs V0V_0 avec barres d'erreur

fig = plt.figure(figsize=(6,6)) # s
ax = plt.subplot() 
ax.errorbar(V,L,e, marker='.', linestyle="none", label="data")
ax.set_title("with error bars")
ax.set_title("L vs $V_0$")
ax.set_xlabel("$V_0$[m/s]")
ax.set_ylabel("L[m]")
ax.legend()

<matplotlib.legend.Legend at 0x7f8428d243a0>

Point 2.3

Utilisez la fonction "curve_fit" pour faire une regression linéaire des données exprimées en une échelle log-log et trouve la valeur de β\beta

popt= curve_fit(func, np.log(V), np.log(L))

popt[0]
a=popt[0][0]
b=popt[0][1]
print("a = %.3f" % a)
print("b = %.3f" % b)

a = 0.991
b = -0.800

Point 2.4

Faites un figure log-log de LL vs V0V_0 en ajoutant la regression linéaire trouvée dans le point précédent

fig = plt.figure(figsize=(6,6)) # s
ax = plt.subplot() 
ax.errorbar(V,L,e, marker='.', linestyle="none", label="data")
ax.plot(V,np.exp(b)*V**a,"-",label="model")
ax.set_title("with error bars")
ax.set_title("L vs $V_0$")
ax.set_xlabel("$V_0$[m/s]")
ax.set_ylabel("L[m]")
ax.legend()
ax.loglog()

[]

Estimation de la constante CC

C1=L/V
print(C1)

0    0.450000
1    0.450000
2    0.446667
3    0.445000
4    0.446667
dtype: float64

print(C.mean(),C1.mean())

0.447073328032969 0.44766666666666677

Le modèle peut s'écrire donc L=CVH1/2L = C V H^{1/2} avec C=0.447C=0.447. L'unité de CC est T2/L\sqrt{T^2/L} L=[C]L/TL1/2 L = [C] L/T L^{1/2}.

Comme le moteur de la chute c'est la gravité et [g]=L/T2[g] = L/T^2 nous pouvons écrire C=2/g C = \sqrt{2/ g} alors L=V02Hg L = V_0 \sqrt{ \frac{2 H}{g}}.